Implementation of Online Shortest Path Computation Based On Live
←
→
Page content transcription
If your browser does not render page correctly, please read the page content below
ISSN 2321-8665
Vol.03,Issue.06,
WWW.IJITECH.ORG August-2015,
Pages:0974-0979
Implementation of Online Shortest Path Computation Based On Live
Traffic Index (LTI)
GAJJA SWAPNA1, GARIKINA BABJI2
1
PG Scholar, Dept of CSE, Harshith Group of Institutions, Hyderabad, TS, India, E-mail: gajjaswapna@gmail.com.
2
Assistant Professor, Dept of CSE, Harshith Group of Institutions, Hyderabad, TS, India, E-mail: garikina.babji@gmail.com.
Abstract: The online shortest path problem aims at path between any pair of places throughout the day.
computing the shortest path based on live traffic Specifically, the quickest path from one place to another
circumstances. This is very important in modern car varies depending on the departure-time from the source.
navigation systems as it helps drivers to make sensible To the best knowledge, this problem has not received much
decisions. To our best knowledge, there is no efficient attention and the costs of answering such continuous queries
system/solution that can offer affordable costs at both client vary hugely in different system architectures. Typical client-
and server sides for online shortest path computation. server architecture can be used to answer shortest path
Unfortunately, the conventional client-server architecture queries on live traffic data. In this case, the navigation system
scales poorly with the number of clients. A promising typically sends the shortest path query to the service provider
approach is to let the server collect live traffic information and waits the result back from the provider (called result
and then broadcast them over radio or wireless network. This transmission model). However, given the rapid growth of
approach has excellent scalability with the number of clients. mobile devices and services, this model is facing scalability
Thus, we develop a new framework called live traffic index limitations in terms of network bandwidth and server loading.
(LTI) which enables drivers to quickly and effectively collect
the live traffic information on the broadcasting channel. An
impressive result is that the driver can compute/update their
shortest path result by receiving only a small fraction of the
index. The experimental study shows that LTI is robust to
various parameters and it offers relatively short tune-in cost
(at client side), fast query response time (at client side), small
broadcast size (at server side), and light maintenance time (at
server side) for online shortest path problem. The existing
systems were infeasible to solve the problem due to their
prohibitive maintenance time and large transmission
overhead. LTI-TD is a novel solution for Online Shortest
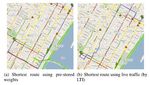
Path Computation on Time Dependent Network. Fig.1. Two alternative shortest paths in Manhattan, NY.
Keywords: Shortest Path, Air Index, And Broadcasting. Based on a telecommunication expert the world’s cellular
networks need to provide 100 times the capacity in 2015
I. INTRODUCTION when compared to the networks in 2011. Furthermore, live
With the popularity of online map applications and their traffic is updated frequently as these data can be collected by
wide deployment in mobile devices and car-navigation using crowd sourcing techniques (e.g., anonymous traffic
systems, an increasing number of users search for point-to- data from Google map users on certain mobile devices). As
point fastest paths and the corresponding travel-times. This such, huge communication cost will be spent on sending
problem has been extensively studied on static road networks result paths on the model as shown in Fig.1. Obviously, the
where edge costs are constant. Many efficient speed-up client-server architecture will soon become impractical in
techniques have been developed to compute the fastest path dealing with massive live traffic in near future. Client-server
in a matter of milliseconds. The quickest path approaches architecture, it cannot scale well with a large number of users.
make the assumption that the travel-time for each edge of the In addition, the reported paths are approximate results and the
road network is constant. In real-world the actual travel-time system does not provide any accuracy guarantee. An
on a road heavily depends on the traffic congestion and, alternative solution is to broadcast live traffic data over
therefore, it is time-dependent. One can observe that the time- wireless network (e.g., 3G, LTE, Mobile WiMAX, etc.). The
dependent travel-times yield a change in the actual quickest navigation system receives the live traffic data from the
Copyright @ 2015 IJIT. All rights reserved.GAJJA SWAPNA, GARIKINA BABJI
broadcast channel and executes the computation locally graph p-Laplacian to the optimal Cheeger cut. The
(called raw transmission model). The traffic data are isoperimetric inequality becomes tight as p, so that the second
broadcasted by a sequence of packets for each broadcast Eigen value converges to the optimal Cheeger cut value.
cycle. To answer shortest path queries based on live traffic
circumstances, the navigation system must fetch those B. SHARC: Fast and Robust Unidirectional Routing
updated packets for each broadcast cycle. The main challenge Introduce SHARC-Routing, a fast and robust approach
on answering live shortest paths is scalability, in terms of the for unidirectional routing in large networks. The central idea
number of clients and the amount of live traffic updates. A of SHARC (Shortcuts + Arc- Flags) is the adaptation of
new and promising solution to the shortest path computation techniques developed for Highway Hierarchies to Arc Flags.
is to broadcast an air index over the wireless network (called In general, SHARC-Routing iteratively constructs a
index transmission model). contraction-based hierarchy during preprocessing and
automatically sets arc- ags for edges removed during
The main advantages of this model are that the network contraction. More precisely, arc- ags are set in such a way
overhead is independent of the number of clients and every that a unidirectional query considers these removed
client only downloads a portion of the entire road map component-edges only at the beginning and the end of a
according to the index information. For instance, the query as a result, able to route very efficiently in scenarios
proposed index constitutes a set of pair wise minimum and where other techniques fail due to their bidirectional nature. It
maximum traveling costs between every two sub partitions of turned out that SHARC was a promising candidate for routing
the road map. However, these methods only solve the in time-dependent networks.
scalability issue for the number of clients but not for the
amount of live traffic updates. As reported the re computation C. Computing point to point shortest path from External
time of the index takes 2 hours for the San Francisco (CA) Memory
road map. It is prohibitively expensive to update the index for The ALT algorithm for the point-to-point shortest path
OSP, in order to keep up with live traffic circumstances. problem in the context of road networks the suggest
Motivated by the lack of off-the-shelf solution for OSP, improvements to the algorithm itself and to its preprocessing
Anew solution based on the index transmission model by stage. Also develop a memory-efficient implementation of
introducing live traffic index (LTI) as the core technique. LTI the algorithm that runs on a Pocket PC (Personal Computer).
is expected to provide relatively short tune-in cost (at client It stores graph data in a ash memory card and uses RAM
side), fast query response time (at client side), small (Random Access Memory) to store information only for the
broadcast size (at server side), and light maintenance time (at part of the graph visited by the current shortest path
server side) for OSP. LTI features as follows. computation. The implementation works even on very large
graphs, including that of the North America road network,
The index structure of LTI is optimized by two novel with almost 30 million vertices.
techniques, graph partitioning and stochastic-based
construction, after conducting a thorough analysis on the D. Time-Dependent SHARC-Routing
hierarchical index techniques. To the best of our knowledge, During the last years, many speed-up techniques for
this is the first work to give a thorough cost analysis on the Dijkstra”s algorithm have been developed. As a result,
hierarchical index techniques and apply stochastic process to computing a shortest path in a static road network is a matter
optimize the index hierarchical structure. LTI efficiently of microseconds. However, only few of those techniques
maintains the index for live traffic circumstances by work in time-dependent networks. Unfortunately, such
incorporating Dynamic Shortest Path Tree (DSPT) into networks appear frequently in reality.
hierarchical index techniques. LTI reduces the tune-in cost up
to an order of magnitude as compared to the state-of-the-art E. Shortest Path Tree Computation in Dynamic Graphs
competitors; while it still provides competitive query The Dynamic Shortest Path (DSP) problem is to compute S
response time, broadcast size, and maintenance time as from D. This problem either focuses on a single edge weight
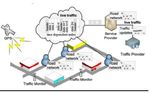
shown in Fig.2. To the best of our knowledge, we are the first change, or for multiple edge weight changes, some of them
work that attempts to minimize all these performance factors are incorrect or are not optimized. The correct and extend a
for OSP. The rest of the paper is organized as follows. few state-of-the-art dynamic SPT algorithms to handle
Literature Survey in SectionII LTI-TD Framework in Section multiple edge weight updates. Hence prove that these
III Experimental Evaluation in SectionIV Finally, our work is algorithms are correct dynamic algorithms may not out
concluded in SectionV. perform static algorithms all the time to evaluate the proposed
dynamic algorithms, compare them with the well-known
II. LITERATURE SURVEY static Dijkstra”s algorithm.
A. Spectral Clustering Based on the Graph Laplacian
A connection between the Cheeger cut and the second III. LTI-TD FRAMEWORK
eigenvector of the graph p-Laplacian, a nonlinear The broadcasting model uses transmission medium such as
generalization of the graph Laplacian. A p-Laplacian which is 3G, Mobile WiMAX. When the traffic provider broadcasts a
slightly from the one used has been used for semi supervised dataset all drivers can listen to the dataset concurrently thus,
learning .The main motivation for the use of eigenvectors of this transmission model balances well independent of the
the graph p-Laplacian was the generalized isoperimetric number of driver. In the wireless broadcast model the traffic
inequality. In which relates the second eigenvalue of the provider repeatedly transmits broadcast cycles, containing the
International Journal of Innovative Technologies
Volume.03, Issue No.06, August-2015, Pages: 0974-0979Implementation of Online Shortest Path Computation Based On Live Traffic Index (LTI)
database and air index. The broadcast cycle consists of fixed- Algorithm ALT (graph G = (V, E), Vertices s and t):
size packets. The most common wireless broadcasting
method is the (1, m) interleaving scheme, shown in Fig.3. 1: L = generate Landmarks (G, k) {select set of k and mark}
2: for all v ∈ V do
3: parent (v) ← ⊥
4: state (v) ← unreached
5: dist(s, v) ← ∞
6: dist(s, s) ← 0
7: state(s) ← reached
8: while vertex v with state (v) = reached exists and state (t)
6= reached do
9: Select v ∈ V with state (v) = reached and minimal cost (v)
= dist(s, v) + πLt (v)
10: for all u ∈ V with (v, u) ∈ E do
Fig.2. System architecture for LTI-TD. 11: if dist(s, v) + len (v, u) + πLt (u)GAJJA SWAPNA, GARIKINA BABJI
our proposed live traffic index are applicable to index values (in bold). In each experiment, we vary a single
transmission model. We omit some methods (such as TNR parameter, while setting the others to their default values. For
[2], Quad tree, SHARC, and CALT) due to their prohibitive each method, we measure its performance in terms of tune-in
maintenance time and broadcast size. In the following, we size, query response time, broadcast size, and index
first describe the road map data used in experiments and maintenance time for all tested methods, and report its
describe the simulation of clients’ movements and live traffic average performance over 2,000 shortest path queries. The
circumstances on a road map. Then, we study the response time is the query computation time at client and the
performance of the above methods with respect to various maintenance time is the index maintenance time at service
factors. provider. In order to measure the exact transmission behavior,
we use the number of packets received (broadcasted) by
Map Data: We test with four different road maps, including client (service provider) to represent the tune-in (broadcast)
New York City (NYC) (264k nodes, 733k edges), San performance. Each packet size is of 128 bytes and the packet
Francisco bay area road map (SF) (174k nodes, 443k edges), format can be found. Each edge weight occupies 4 bytes. For
San Joaquin road map (SJ) (18k nodes, 48k edges), and Algorithm 1, we randomly generate 1,000 queries at each
Oldenburg road map (OB) (6k nodes, 14k edges). All of them Monte Carlo estimation and we only partition the graph into 2
are available. to 16 sub graphs at every partitioning for boosting up the
construction time. As a remark, each sub graph/partition (in
Simulation Of Clients And Traffic Updates: We run the the Hi-Ti and LTI methods) may span over multiple packets.
network based generator to generate the weight of edges. It
initializes 100,000 cars (i.e., clients) and then generates 1,000 A. Effectiveness of Optimizations
new cars in each iteration. It runs for 200 iterations in total, First, we evaluate the effectiveness of the optimizations
with the other generator parameters as their default values. proposed. The fully optimized LTI is compared against to
The weight of an edge is set to the average driving time on it. LTI-bi Part (that is constructed by only the graph partitioning
technique, described) and Hi-Ti (which is the most
We adopt the approach into simulate live traffic updates. representative model of hierarchical index structures). For
The initial weights of edges are assigned by the above fairness, we internally tune the Hi-Ti graph model by varying
network-based generator. In each iteration, we randomly the number of children sub graphs, and the eight-way regular
select a set of edges subject to the update ratio d and specific partitioning is the best Hi-Ti graph model among all testing’s.
weight update settings. In our work, each weight update can
be a light traffic change, a heavy traffic change, or road
maintenance. The proportion of these update types are β, ,
and , respectively, where β is a ratio parameter. For each
light traffic change, the edge weight is set to ±20% of the
current weight. For each heavy traffic change, the weight is
set to a large value by multiplying a weight factor v (which is
set to 5 by default) for each road maintenance the weight is
set to 1. We reset the edge weight to its initial value if the
edge weight is updated by heavy traffic or road maintenance
after 10 iterations.
TABLE I: Range of Parameter Values Fig.4. Varying number of partitions, γ.
TABLE II: Performance of Different Methods
Implementation and Evaluation Platforms: All tested
methods except CH were implemented in Java. Experiments
on the service provider were conducted on an Intel Xeon
E5620 2.40 GHz CPU machine with 18 G Bytes memory,
running Ubuntu 10.10; and experiments on the client were
performed on an Intel Core2Duo 2.66 GHz CPU machine
with 4 G Bytes memory, running Windows 7. Table 1 shows
the ranges of the investigated parameters, and their default
International Journal of Innovative Technologies
Volume.03, Issue No.06, August-2015, Pages: 0974-0979Implementation of Online Shortest Path Computation Based On Live Traffic Index (LTI)
Fig. 4 plots the performance of all three methods as a important since reducing the tune-in cost provides
function of the number of partitions g on the SF data set. For opportunity for clients to receive more services
the sake of saving space, we plot the costs at service provider simultaneously by selective tuning. In addition, fast
(i.e., broadcast size and maintenance time) into one figure maintenance time keeps the freshness of the broadcasted
and plot the costs at client (i.e., tune-in size and response index. The maintenance time of LTI is 2.58-6.5 times faster
time) into another figure. The number of packets (left y-axis) than CH while the broadcast size of LTI is just 23.6 and 40
is represented by bars, whereas the time (right y-axis) is percent larger than CH in NYC and SF, respectively. We
represented by lines. LTI is superior to LTI-bi-Part and Hi-Ti show that the present traffic providers report the traffic very
for all four performance factors in Fig. 4. As compared to Hi- frequently and megabit wireless networks (3G, LTE, Mobile
Ti, its maintenance time and response time are up to 14.7 and WiMAX, etc.) are available. Therefore, the maintenance time
21.1 times faster, respectively. The broadcast size and tune-in of LTI (i.e., 2 and 5.5 seconds on SF and NYC, respectively)
size are at least 2.4 and 6.4 times smaller than Hi-Ti. It shows is affordable as compared to the live traffic update frequency
that our fully optimized LTI is very efficient and performs and the broadcast overhead of LTI (i.e., around 35 percent
vastly different from Hi-Ti. In this work, we set g to 1,000 larger than the raw data) is reasonable as the data is
since it performs the best in both Hi-Ti and LTI. As shown in transmitted on the megabit wireless networks.
the figures, all performance factors are not very sensitive to g
which supports our claim. We omit Hi-Ti from the remaining experiments as it is
inferior to LTI. The remaining representative methods are:
B. Scalability Experiments DALT on the raw transmission model, CH and LTI on the
Next, we compare the discussed solutions on four index transmission model we evaluate the performance of
different road maps. The result is shown in Table 2. Note that these three methods as a function of different system settings
all methods on the raw transmission model have the same in Fig. 5. In Fig. 5a, the tune-in size of all methods grow with
tune-in size and broadcast size. The only difference is the the update ratio d, as well, the response time slightly
response time as it represents the local computation time for increases since the search graph becomes larger. When δ=
each client. Apart from BD and DALT, other methods require 20%, the number of necessary packets received by clients is
each client to maintain some index structures locally after 13847.2, 13390.12, and 727.28 for DALT, CH, and LTI
receiving the live traffic updates. Thus, their response time is respectively. DALT and CH almost receive the entire
slower5 than BD and DALT on the raw transmission model. broadcast packets (i.e., 99.89 and 99.53 percent,
Based on the response time, DALT is the best approach respectively); this conforms to our edge-update probability
among the methods in this category. analysis. An impressive finding is that the client using LTI
only receives 20.63 percent more packets as compared to δ =
10%. This shows that LTI is robust as the tune-in size only
increases sub-linearly with the update ratio δ.
Fig.5. Scalability experiments (client).
Regarding the index transmission model, Hi-Ti is Fig.6. Scalability experiments (service provider).
obviously infeasible for online shortest path computation due
to its prohibitive costs. Although CH has slightly better Fig.5b shows the tune-in size and response time of the
broadcast size and response time, 6 we recommend LTI as the methods on different type of shortest path queries s. The type
best approach due to its light tune-in cost and fast of queries is classified based on their length. Again, LTI has
maintenance time. The tune-in size significantly affects the the lowest tune-in cost which is at least 16.9 times smaller
energy consumption and the duration of active mode at client than DALT and CH among all three types of queries. Note
receiver. The tune-in size of LTI is 2.19-26.41 and 2.97-25.97 that only DALT is sensitive to various lengths of queries to
times smaller than CH and DALT, respectively. Note that the the response time since the distance bounds derived from the
margin becomes more significant on larger maps which pre-computed information become looser when the length of
demonstrate good scalability of our LTI framework. This is queries is longer. We then study how the methods perform for
International Journal of Innovative Technologies
Volume.03, Issue No.06, August-2015, Pages: 0974-0979GAJJA SWAPNA, GARIKINA BABJI
different traffic circumstances. Figs. 5c and 5d shows the implementation details and results are not given. In the future,
tune-in size and response time of the methods on two traffic extend this solution on time dependent networks. This is a
update behaviors. For all three methods, the tune-in size and very interesting topic since the decision of a shortest path
response time are not very sensitive to the ratio of traffic depends not only on current traffic data but also based on the
updates β and the weight factor of heavy traffic ω. Again, our predicted traffic circumstances.
LTI outperforms DALT and CH by an order of magnitude in
terms of the tune-in size. VI. REFERENCES
[1] Leong Hou U, Hong Jun Zhao, Man Lung Yiu, Yuhong
Lastly, we demonstrate how the methods perform at Li, and Zhiguo Gong, “Towards Online Shortest Path
service provider. Fig. 6 shows the broadcast size and Computation”, IEEE Transactions on Knowledge and Data
maintenance time of the methods by varying δ, σ, β, and v. Engineering, Vol. 26, No. 4, April 2014.
For all testing’s, LTI is superior to CH in terms of [2] H. Bast, S. Funke, D. Matijevic, P. Sanders, and D.
maintenance time but produces around 40 percent more Schultes, “In Transit to Constant Time Shortest-Path Queries
packets than CH. A more promising result is that the in Road Networks,” Proc. Workshop Algorithm Eng. and
maintenance time of LTI is no longer sensitive to the update Experiments (ALENEX), 2007.
ratio when δ > 20%. This is because most of BSPTs are [3] P. Sanders and D. Schultes, “Engineering Highway
necessarily updated when the update ratio is around 20 Hierarchies,” Proc. 14th Conf. Ann. European Symp. (ESA),
percent. The subsequent updates (> 20%) are more likely pp. 804-816, 2006.
some incremental work in updating the BSPTs (i.e., [4] G. Dantzig, Linear Programming and Extensions, series
traversing few more edges by the Dijkstra like algorithm) so Rand Corporation Research Study Princeton Univ. Press,
that it becomes less sensitive to δ. To express the comparison 1963.
in absolute terms, we show the time [5] R.J. Gutman, “Reach-Based Routing: A New Approach to
Shortest Path Algorithms Optimized for Road Networks,”
TABLE III: Broadcast Cycle Length at Default Settings Proc. Sixth Workshop Algorithm Eng. and Experiments and
the First Workshop Analytic Algorithmics and Combinatorics
(ALENEX/ANALC), pp. 100-111, 2004.
[6] B. Jiang, “I/O-Efficiency of Shortest Path Algorithms: An
Analysis,” Proc. Eight Int’l Conf. Data Eng. (ICDE), pp. 12-
19, 1992.
[7] P. Sanders and D. Schultes, “Highway Hierarchies Hasten
Exact Shortest Path Queries,” Proc. 13th Ann. European
it takes to broadcast over a 1.92 Mbps (WCDMA) and a 14 Conf. Algorithms (ESA), pp. 568-579, 2005.
Mbps (HSDPA) channel in Table 3, which are typical [8] D. Schultes and P. Sanders, “Dynamic Highway-Node
transmission rates in 3G networks and 3.5G networks. LTI Routing,” Proc. Sixth Int’l Conf. Experimental Algorithms
takes 11.6 and 3.32 s to complete maintenance and broadcast (WEA), pp. 66-79, 2007.
cycle at WCDMA and HSDPA, respectively; while CH takes [9] F. Zhan and C. Noon, “Shortest Path Algorithms: An
12.25 and 6.35 s to complete the same cycle, respectively. In Evaluation Using Real Road Networks,” Transportation
addition, DALT and CH require the clients to tune-in the Science, vol. 32, no. 1, pp. 65-73, 1998.
broadcast channel for ~5 and ~0.7 s over WCDMA and [10] “Google Maps,” http://maps.google.com, 2014.
HSDPA, respectively, which significantly affects the number [11] “NAVTEQ Maps and Traffic,” http://www.navteq.com,
of simultaneous services in the wireless broadcast 2014.
environments. Although DALT does not bother any [12] “INRIX Inc. Traffic Information Provider,”
maintenance cost at service provider, the tune-in cost and http://www.inrix. com, 2014.
response time of DALT makes it infeasible on the live traffic
circumstance. Author’s Profile:
Gajja Swapna, 1PG Scholar, Dept of
V. CONCLUSION CSE, Harshith Group of Institutions,
The online shortest path computation; the shortest path Hyderabad, TS, India,
result is computed/updated based on the live traffic E-mail: gajjaswapna@gmail.com.
circumstances. Analyze the existing work and discuss their
inapplicability to the problem (due to their prohibitive
maintenance time and large transmission overhead). To
address the problem of efficient fastest path in modern Garikina Babji, Assistant Professor,
navigation systems in the presence of varying speed Dept of CSE, Harshith Group of
conditions on a large scale road network, a promising Institutions, Hyderabad, TS, India,
architecture that broadcasts the index on the air depending on E-mail: garikina.babji@gmail.com
time is required. The existing systems were infeasible to
solve the problem due to their prohibitive maintenance time
and large transmission overhead. LTI-TD is a novel solution
for Online Shortest Path Computation on Time Dependent
Network. Since a system is currently under development
International Journal of Innovative Technologies
Volume.03, Issue No.06, August-2015, Pages: 0974-0979You can also read