Reinforcement Learning for Non-Stationary Markov Decision Processes: The Blessing of (More) Optimism
←
→
Page content transcription
If your browser does not render page correctly, please read the page content below
Reinforcement Learning for Non-Stationary Markov Decision Processes:
The Blessing of (More) Optimism
Wang Chi Cheung 1 David Simchi-Levi 2 Ruihao Zhu 2
Abstract imizes its cumulative rewards, while facing the following
challenges:
We consider un-discounted reinforcement learn-
ing (RL) in Markov decision processes (MDPs) • Endogeneity: At each time step, the reward follows a
under drifting non-stationarity, i.e., both the re- reward distribution, and the subsequent state follows a
ward and state transition distributions are allowed state transition distribution. Both distributions depend
to evolve over time, as long as their respective (solely) on the current state and action, which are influ-
total variations, quantified by suitable metrics, do enced by the policy. Hence, the environment can be fully
not exceed certain variation budgets. We first characterized by a discrete time Markov decision process
develop the Sliding Window Upper-Confidence (MDP).
bound for Reinforcement Learning with Confi- • Exogeneity: The reward and state transition distributions
dence Widening (SWUCRL2-CW) algorithm, and vary (independently of the policy) across time steps, but
establish its dynamic regret bound when the vari- the total variations are bounded by the respective variation
ation budgets are known. In addition, we propose budgets.
the Bandit-over-Reinforcement Learning (BORL) • Uncertainty: Both the reward and state transition distri-
algorithm to adaptively tune the SWUCRL2-CW butions are initially unknown to the DM.
algorithm to achieve the same dynamic regret • Bandit/Partial Feedback: The DM can only observe the
bound, but in a parameter-free manner, i.e., with- reward and state transition resulted by the current state
out knowing the variation budgets. Notably, learn- and action in each time step.
ing non-stationary MDPs via the conventional op- It turns out that many applications, such as real-time bid-
timistic exploration technique presents a unique ding in advertisement (ad) auctions, can be captured by this
challenge absent in existing (non-stationary) ban- framework (Cai et al., 2017; Flajolet & Jaillet, 2017; Bal-
dit learning settings. We overcome the challenge seiro & Gur, 2019; Guo et al., 2019; Han et al., 2020).
by a novel confidence widening technique that Besides, this framework can be used to model sequen-
incorporates additional optimism. tial decision-making problems in transportation (Zhang &
Wang, 2018; Qin et al., 2019), wireless network (Zhou &
Bambos, 2015; Zhou et al., 2016), consumer choice model-
1. Introduction ing (Xu & Yun, 2020), ride-sharing (Taylor, 2018; Gurvich
et al., 2018; Bimpikis et al., 2019; Kanoria & Qian, 2019),
Consider a general sequential decision-making framework, healthcare operations (Shortreed et al., 2010), epidemic con-
where a decision-maker (DM) interacts with an initially un- trol (Nowzari et al., 2016; Kiss et al., 2017), and inventory
known environment iteratively. At each time step, the DM control (Huh & Rusmevichientong, 2009; Bertsekas, 2017;
first observes the current state of the environment, and then Zhang et al., 2018; Agrawal & Jia, 2019; Chen et al., 2019a).
chooses an available action. After that, she receives an in-
stantaneous random reward, and the environment transitions There exists numerous works in sequential decision-making
to the next state. The DM aims to design a policy that max- that considered part of the four challenges. The traditional
stream of research (Auer et al., 2002a; Bubeck & Cesa-
1
Department of Industrial Systems Engineering and Manage- Bianchi, 2012; Lattimore & Szepesvári, 2018) on stochastic
ment, National University of Singapore 2 MIT Institute for Data, multi-armed bandits (MAB) focused on the interplay be-
Systems, and Society. Correspondence to: Wang Chi Cheung
, David Simchi-Levi , tween uncertainty and bandit feedback (i.e., challenges 3
Ruihao Zhu . and 4), and (Auer et al., 2002a) proposed the classical Upper
Confidence Bound (UCB) algorithm. Starting from (Bur-
Proceedings of the 37 th International Conference on Machine netas & Katehakis, 1997; Tewari & Bartlett, 2008; Jaksch
Learning, Vienna, Austria, PMLR 119, 2020. Copyright 2020 by et al., 2010), a volume of works (see Section 3) have been
the author(s).Non-Stationary Reinforcement Learning
Stationary Non-stationary
MAB OFU (Auer et al., 2002a) OFU + Forgetting (Besbes et al., 2014; Cheung et al., 2019b)
RL OFU (Jaksch et al., 2010) Extra optimism + Forgetting (This paper)
Table 1. Summary of algorithmic frameworks of stationary and non-stationary online learning settings.
devoted to reinforcement learning (RL) in MDPs (Sutton 2010) to RL in non-stationary MDPs may result in poor
& Barto, 2018), which further involves endogeneity. RL in dynamic regret bounds.
MDPs incorporate challenges 1,3,4, and stochastic MAB is
a special case of MDPs when there is only one state. In the 1.1. Summary of Main Contributions
absence of exogeneity, the reward and state transition distri-
butions are invariant across time, and these three challenges Assuming that, during the T time steps, the total variations
can be jointly solved by the Upper Confidence bound for of the reward and state transition distributions are bounded
Reinforcement Learning (UCRL2) algorithm (Jaksch et al., (under suitable metrics) by the variation budgets Br (> 0)
2010). and Bp (> 0), respectively, we design and analyze novel
algorithms for RL in non-stationary MDPs. Let Dmax , S,
The UCB and UCRL2 algorithms leverage the optimism and A be respectively the maximum diameter (a complexity
in face of uncertainty (OFU) principle to select actions it- measure to be defined in Section 2), number of states, and
eratively based on the entire collections of historical data. number of actions in the MDP. Our main contributions are:
However, both algorithms quickly deteriorate when exo-
• We develop the Sliding Window UCRL2 with Con-
geneity emerge since the environment can change over time,
fidence Widening (SWUCRL2-CW) algorithm. When
and the historical data becomes obsolete. To address the
the! variation budgets are known, we "prove it attains a
challenge of exogeneity, (Garivier & Moulines, 2011b) con-
Õ Dmax (Br + Bp )1/4 S 2/3 A1/2 T 3/4 dynamic regret
sidered the piecewise-stationary MAB environment where
bound via a budget-aware analysis.
the reward distributions remain unaltered over certain time
• We propose the Bandit-over-Reinforcement Learning
periods and change at unknown time steps. Later on, there is
(BORL) algorithm that tunes the SWUCRL2-CW
a line of research initiated by (Besbes et al., 2014) that stud-
algorithm adaptively, and retains the same
ied the general non-stationary MAB environment (Besbes ! "
Õ Dmax (Br + Bp )1/4 S 2/3 A1/2 T 3/4 dynamic
et al., 2014; Cheung et al., 2019a;b), in which the reward
regret bound without knowing the variation budgets.
distributions can change arbitrarily over time, but the total
• We identify an unprecedented challenge for RL in non-
changes (quantified by a suitable metric) is upper bounded
stationary MDPs with conventional optimistic exploration
by a variation budget (Besbes et al., 2014). The aim is to
techniques: existing algorithmic frameworks for non-
minimize the dynamic regret, the optimality gap compared
stationary online learning (including non-stationary ban-
to the cumulative rewards of the sequence of optimal actions.
dit and RL in piecewise-stationary MDPs) (Jaksch et al.,
Both the (relatively restrictive) piecewise-stationary MAB
2010; Garivier & Moulines, 2011b; Cheung et al., 2019a)
and the general non-stationary MAB settings consider the
typically estimate unknown parameters by averaging his-
challenges of exogeneity, uncertainty, and partial feedback
torical data in a “forgetting” fashion, and construct the
(i.e., challenges 2, 3, 4), but endogeneity (challenge 1) are
tightest possible confidence regions/intervals accordingly.
not present.
They then optimistically search for the most favorable
In this paper, to address all four above-mentioned chal- model within the confidence regions, and execute the
lenges, we consider RL in non-stationary MDPs where bot corresponding optimal policy. However, we first demon-
the reward and state transition distributions can change over strate in Section 4.1, and then rigorously show in Section
time, but the total changes (quantified by suitable metrics) 6 that in the context of RL in non-stationary MDPs, the
are upper bounded by the respective variation budgets. We diameters induced by the MDPs in the confidence regions
note that in (Jaksch et al., 2010), the authors also consider constructed in this manner can grow wildly, and may re-
the intermediate RL in piecewise-stationary MDPs. Never- sult in unfavorable dynamic regret bound. We overcome
theless, we first demonstrate in Section 4.1, and then rigor- this with our novel proposal of extra optimism via the
ously show in Section 6 that simply adopting the techniques confidence widening technique (alternatively, in (Cheung
for non-stationary MAB (Besbes et al., 2014; Cheung et al., et al., 2020a), an extended version of the current paper,
2019a;b) or RL in piecewise-stationary MDPs (Jaksch et al., the authors demonstrate that one can leverage specialNon-Stationary Reinforcement Learning
structures on the state transition distributions in the con- DM, individual Br,t ’s and Bp,t ’s are unknown to the DM
text of single item inventory control with fixed cost to throughout the current paper.
bypass this difficulty of exploring time-varying environ-
Endogeneity: The DM faces a non-stationary MDP in-
ments). A summary of the algorithmic frameworks for
stance (S, A, T, r, p). She knows S, A, T , but not r, p.
stationary and non-stationary online learning settings are
The DM starts at an arbitrary state s1 œ S. At time t,
provided in Table 1.
three events happen. First, the DM observes its current
state st . Second, she takes an action at œ Ast . Third,
2. Problem Formulation given st , at , she stochastically transits to another state st+1
which is distributed as pt (·|st , at ), and receives a stochas-
In this section, we introduce the notations to be used
tic reward Rt (st , at ), which is 1-sub-Gaussian with mean
throughout paper, and introduce the learning protocol for
rt (st , at ). In the second event, the choice of at is based on
our problem of RL in non-stationary MDPs.
a non-anticipatory policy . That is, the choice only de-
pends on the current state st and the previous observations
2.1. Notations Ht≠1 := {sq , aq , Rq (sq , aq )}t≠1
q=1 .
Throughout the paper, all vectors are column vectors, unless Dynamic Regret: The q DM aims to maximize the cumula-
specified otherwise. We define [n] to be the set {1, 2, . . . , n} tive expected reward E[ t=1 rt (st , at )], despite the model
T
for any positive integer n. We denote 1[·] as the indicator uncertainty on r, p and the dynamics of the learning envi-
function. For p œ [1, Œ], we use ÎxÎp to denote the p-norm ronment. To measure the convergence to optimality, we
of a vector x œ Rd . We denote x ‚ y and x · y as the max- consider an equivalent objective of minimizing the dynamic
imum and minimum between x, y œ R, respectively. We regret (Besbes et al., 2014; Jaksch et al., 2010)
adopt the asymptotic notations O(·), (·), and (·) (Cor-
T
ÿ
men et al., 2009). When logarithmic factors are omitted, we
use Õ(·), ˜ (·), ˜ (·), respectively. With some abuse, these Dyn-RegT ( ) = {flút ≠ E[rt (st , at )]} . (2)
t=1
notations are used when we try to avoid the clutter of writing
qT
out constants explicitly. In the oracle t=1 flút , the summand flút is the optimal long-
term average reward of the stationary MDP with state tran-
2.2. Learning Protocol sition distribution pt and mean reward rt . The optimum flút
can be computed by solving linear program (9) provided in
Model Primitives: An instance of non-stationary MDP
Section A.1. We note that the same oracle is used for RL in
is specified by the tuple (S, A, T, r, p). The set S is a fi-
piecewise-stationary MDPs (Jaksch et al., 2010).
nite set of states. The collection A = {As }sœS contains
a finite action set As for each state s œ S. We say that Remark 1. When S = 1, (2) reduces to the definition
(s, a) is a state-action pair (Besbes et al., 2014) of dynamic regret for non-stationary
q if s œ S, a œ As . We de- K-armed bandits. Nevertheless,
note S = |S|, A = ( sœS |As |)/S. We denote T as qT different from the bandit
the total number of time steps, and denote r = {rt }Tt=1 case, the offline benchmark t=1 flút does not equal to the
as the sequence of mean rewards. For each t, we have expected optimum for the non-stationary MDP problem in
rt = {rt (s, a)}sœS,aœAs , and rt (s, a) œ [0, 1] for each general. We justify our choice in Proposition 1.
state-action pair (s, a). In addition, we denote p = {pt }Tt=1 Next, we review concepts of communicating MDPs and
as the sequence of state transition distributions. For each diameters, in order to stipulate an assumption that ensures
t, we have pt = {pt (·|s, a)}sœS,aœAs , where pt (·|s, a) is learnability and justifies our offline bnechmark.
a probability distribution over S for each state-action pair
(s, a). Definition 1 ((Jaksch et al., 2010) Communicating
MDPs and Diameters). Consider a set of states S,
Exogeneity: The quantities rt ’s and pt ’s vary across dif- a collection A = {As }sœS of action sets, and a
ferent t’s in general. Following (Besbes et al., 2014), we transition kernel p̄ = {p̄(·|s, a)}sœS,aœAs . For any
quantify the variations on rt ’s and pt ’s in terms of their s, sÕ œ S and stationary policy fi, the hitting time from
respective variation budgets Br , Bp (> 0): s to sÕ under fi is the random variable (sÕ |fi, s) :=
min {t : st+1 = sÕ , s1 = s, s· +1 ≥ p̄(·|s· , fi(s· )) ’· } ,
T
ÿ ≠1 T
ÿ ≠1
which can be infinite. We say that (S, A, p̄) is a
Br = Br,t , Bp = Bp,t , (1) communicating MDP iff
t=1 t=1
D := max min E [ (sÕ |fi, s)]
where Br,t = maxsœS,aœAs |rt+1 (s, a) ≠ rt (s, a)| and s,s œS stationary fi
Õ
Bp,t = maxsœS,aœAs Îpt+1 (·|s, a) ≠ pt (·|s, a)Î1 . We em- is finite. The quantity D is the diameter associated with
phasize although Br and Bp might be used as inputs by the (S, A, p̄).Non-Stationary Reinforcement Learning
We make the following assumption throughout. 3.2. RL in Non-Stationary MDPs
Assumption 1. For each t œ {1, . . . , T }, the tuple In a parallel work (Ortner et al., 2019), the authors consid-
(S, A, pt ) constitutes a communicating MDP with diam- ered a similar setting to ours by applying the “forgetting
eter at most Dt . We denote the maximum diameter as principle” from non-stationary bandit settings (Garivier &
Dmax = maxtœ{1,...,T } Dt . Moulines, 2011b; Cheung et al., 2019b) to design a learn-
ing algorithm. To achieve its dynamic regret bound, the
The following
qT proposition justifies our choice of offline algorithm by (Ortner et al., 2019) partitions the entire time
benchmark t=1 flút . horizon [T ] into time intervals I = {Ik }K , and crucially
qmax Ik ≠1 k=1
qmax Ik ≠1
Proposition 1. Consider an instance (S, A, T, p, r) that requires the access to t=min Ik Br,t and t=min Ik Bp,t ,
satisfies Assumption 1 with maximum diameter Dmax , i.e., the variations in both reward and state transition distribu-
and has variation budgets Br , Bp for the rewards and tions of each interval Ik œ I (see Theorem 3 in (Ortner et al.,
transition kernels respectively. In addition, suppose 2019)). In contrast, the SWUCRL2-CW algorithm and the
that T Ø Br +Ó2D max Bp
Ëq > 0. ÈÔIt holds that BORL algorithm require significantly less information on the
qT variations. Specifically, the SWUCRL2-CW algorithm does
t=1 flt Ø max t=1 rt (st , at ) ≠ 4(Dmax +
T
ú
E
not need any additional knowledge on the variations except
1) (Br + 2Dmax Bp )T . The maximum is taken over all for Br and Bp , i.e., the variation budgets over the entire
non-anticipatory policies ’s. We denote {(st , at )}Tt=1 time horizon as defined in eqn. (1), to achieve its dynamic
as the trajectory under policy , where at œ Ast is regret bound (see Theorem 1). This is similar to algorithms
determined based on and Ht≠1 fi {st }, and st+1 ≥ for the non-stationary bandit settings, which only require
pt (·|st , at ) for each t. the access to Br (Besbes et al., 2014). More importantly,
the BORL algorithm (built upon the SWUCRL2-CW algo-
The Proposition is proved in Section A.2 of the full ver- rithm) enjoys the same dynamic regret bound even without
sion (Cheung et al., 2020b). In fact, our dynamic re- knowing either of Br or Bp (see Theorem 2).
bounds are larger than the error term 4(Dmax +
gret
There also exists some settings that are closely related to,
1) (Br + 2Dmax Bp )T , thus justifying the choice of
qT but different than our setting (in terms of exogeneity and
flút as the offline benchmark. The offline benchmark
qt=1
T feedback). (Jaksch et al., 2010; Gajane et al., 2018) pro-
t=1 flt is more convenient for analysis than the expected
ú
posed solutions for the RL in piecewise-stationary MDPs
optimum, since the former can be decomposed to summa- setting. But as discussed before, simply applying their tech-
tions across different intervals, unlike the latter where the niques to the general RL in non-stationary MDPs may result
summands are intertwined (since st+1 ≥ pt (·|st , at )). in undesirable dynamic regret bounds (see Section 6 for
more details). In (Yu et al., 2009; Neu et al., 2010; Arora
3. Related Works et al., 2012; Dick et al., 2014; Jin et al., 2019; Cardoso et al.,
2019), the authors considered RL in MDPs with changing
3.1. RL in Stationary MDPs reward distributions but fixed transition distributions. The
RL in stationary (discounted and un-discounted reward) authors of (Even-Dar et al., 2005; Yu & Mannor, 2009; Neu
MDPs has been widely studied in (Burnetas & Katehakis, et al., 2012; Abbasi-Yadkori et al., 2013; Rosenberg & Man-
1997; Bartlett & Tewari, 2009; Jaksch et al., 2010; Agrawal sour, 2019; Li et al., 2019) considered RL in non-stationary
& Jia, 2017; Fruit et al., 2018a;b; Sidford et al., 2018b;a; MDPs with full information feedback.
Wang, 2019; Zhang & Ji, 2019; Fruit et al., 2019; Wei et al.,
2019). For the discounted reward setting, the authors of (Sid- 3.3. Non-Stationary MAB
ford et al., 2018b; Wang, 2019; Sidford et al., 2018a) pro-
For online learning and bandit problems where there is
posed (nearly) optimal algorithms in terms of sample com-
only one state, the works by (Auer et al., 2002b; Garivier
plexity. For the un-discounted reward setting, the authors
& Moulines, 2011b; Besbes et al., 2014; Keskin & Zeevi,
of (Jaksch
Ô et al., 2010) established a minimax lower bound
2016) proposed several “forgetting” strategies for different
( Dmax SAT ) on the regret when both the reward and
non-stationary MAB settings. More recently, the works by
state transition distributions are time-invariant. They also
(Karnin & Anava, 2016; Luo et al., 2018; Cheung et al.,
designed the UCRL2 algorithm
Ô and showed that it attains a
2019a;b; Chen et al., 2019b) designed parameter-free algo-
regret bound Õ(Dmax S AT ). The authors of (Fruit et al.,
rithms for non-stationary MAB problems. Another related
2019) proposed the UCRL2B algorithm, which is an im-
but different setting is the Markovian bandit (Kim & Lim,
proved version of the UCRL2 algorithm.
Ô The regret bound
2 2016; Ma, 2018), in which the state of the chosen action
of the UCRL2B algorithm is Õ(S Dmax AT +Dmax S 2 A).
evolve according to an independent time-invariant Markov
The minimax optimal algorithm is provided in (Zhang & Ji,
chain while the states of the remaining actions stay un-
2019) although it is not computationally efficient.Non-Stationary Reinforcement Learning
changed. In (Zhou et al., 2020), the authors also considered the diameter of the estimated MDP produced by the naive
the case when the states of all the actions are governed by sliding-window UCRL2 algorithm with window size W
the same (uncontrollable) Markov chain. can be as large as (W ), which is orders of magnitude
larger than Dmax , the maximum diameter of each individ-
4. Sliding Window UCRL2 with Confidence ual MDP encountered by the DM. Consequently, the naive
sliding-window UCRL2 algorithm may result in undesirable
Widening dynamic regret bound. In what follows, we discuss in more
In this section, we present the SWUCRL2-CW algorithm, details how our novel confidence widening technique can
which incorporates sliding window estimates (Garivier & mitigate this issue.
Moulines, 2011a) and a novel confidence widening tech-
nique into UCRL2 (Jaksch et al., 2010). 4.2. Design Overview
The SWUCRL2-CW algorithm first specifies a sliding win-
4.1. Design Challenge: Failure of Naive Sliding dow parameter W œ N and a confidence widening parame-
Window UCRL2 Algorithm ter ÷ Ø 0. Parameter W specifies the number of previous
For stationary MAB problems, the UCB algorithm (Auer time steps to look at. Parameter ÷ quantifies the amount of
et al., 2002a) suggests the DM should iteratively execute additional optimistic exploration, on top of the conventional
the following two steps in each time step: optimistic exploration using upper confidence bounds. The
former turns out to be necessary for handling the drifting
1. Estimate the mean reward of each action by taking the non-stationarity of the transition kernel.
time average of all observed samples.
2. Pick the action with the highest estimated mean reward The algorithm runs in a sequence of episodes that partitions
plus the confidence radius, where the radius scales in- the T time steps. Episode m starts at time · (m) (in partic-
versely proportional with the number of observations ular · (1) = 1), and ends at the end of time · (m + 1) ≠ 1.
(Auer et al., 2002a). Throughout an episode m, the DM follows a certain station-
ary policy fĩm . The DM ceases the mth episode if at least
The UCB algorithm has been proved to attain optimal regret
one of the following two criteria is met:
bounds for various stationary MAB settings (Auer et al.,
2002a; Kveton et al., 2015). For non-stationary problems, • The time index t is a multiple of W. Consequently, each
(Garivier & Moulines, 2011b; Keskin & Zeevi, 2016; Che- episode last for at most W time steps. The criterion en-
ung et al., 2019b) shown that the DM could further leverage sures that the DM switches the stationary policy fĩm fre-
the forgetting principle by incorporating the sliding-window quently enough, in order to adapt to the non-stationarity
estimator (Garivier & Moulines, 2011b) into the UCB algo- of rt ’s and pt ’s.
rithms (Auer et al., 2002a; Kveton et al., 2015) to achieve • There exists some state-action pair (s, a) such that
optimal dynamic regret bounds for a wide variety of non- ‹m (s, a), the number of time step t’s with (st , at ) =
stationary MAB settings. The sliding window UCB algo- (s, a) within episode m, is at least as many as the total
rithm with a window size W œ R+ is similar to the UCB number of counts for it within the W time steps prior to
algorithm except that the estimated mean rewards are com- · (m), i.e., from (· (m) ≠ W ) ‚ 1 to (· (m) ≠ 1). This is
puted by taking the time average of the W most recent similar to the doubling criterion in (Jaksch et al., 2010),
observed samples. which ensures that each episode is sufficiently long so
that the DM can focus on learning.
As noted in Section 1, (Jaksch et al., 2010) proposed the
UCRL2 algorithm, which is a UCB-alike algorithm with The combined effect of these two criteria allows the DM
nearly optimal regret for RL in stationary MDPs. It is thus to learn a low dynamic regret policy with historical data
tempting to think that one could also integrate the forgetting from an appropriately sized time window. One important
principle into the UCRL2 algorithm to attain low dynamic piece of ingredient is the construction of the policy fĩm , for
regret bound for RL in non-stationary MDPs. In particular, each episode m. To allow learning under non-stationarity,
one could easily design a naive sliding-window UCRL2 the SWUCRL2-CW algorithm computes the policy fĩm based
algorithm that follows exactly the same steps as the UCRL2 on the history in the W time steps previous to the current
algorithm with the exception that it uses only the W most episode m, i.e., from round (· (m)≠W )‚1 to round · (m)≠
recent observed samples instead of all observed samples to 1. The construction of fĩm involves the Extended Value
estimate the mean rewards and the state transition distribu- Iteration (EVI) (Jaksch et al., 2010), which requires the
tions, and to compute the respective confidence radius. confidence regions Hr,· (m) , Hp,· (m) (÷) for rewards and
transition kernels as the inputs, in addition to an precision
Under non-stationarity and bandit feedback, however, we parameter ‘. The confidence widening parameter ÷ Ø 0
show in Proposition 3 of the forthcoming Section 6 that is capable of ensuring the MDP output by the EVI has aNon-Stationary Reinforcement Learning
bounded diameter most of the time. radp,t (s, a) = 2 2S log (SAT /”)/Nt+ (s, a).
4.3. Policy Construction In a nutshell, the incorporation of ÷ > 0 provides an addi-
tional source of optimism, and the DM can explore transition
To describe SWUCRL2-CW algorithm, we define for each kernels that further deviate from the sample average. This
state action pair (s, a) and each round t in episode m, turns out to be crucial for learning MDPs under drifting
t≠1 non-stationarity. We treat ÷ as a hyper-parameter at the mo-
ÿ
Nt (s, a) = 1((sq , aq ) = (s, a)), ment, and provide a suitable choice of ÷ when we discuss
q=(· (m)≠W )‚1
our main results.
Nt+ (s, a) = max{1, Nt (s, a)}. (3) 4.3.3. E XTENDED VALUE I TERATION (EVI) (JAKSCH
ET AL ., 2010).
4.3.1. C ONFIDENCE R EGION FOR R EWARDS .
The SWUCRL2-CW algorithm relies on the EVI, which
For each state action pair (s, a) and each time step t in solves MDPs with optimistic exploration to near-optimality.
episode m, we consider the empirical mean estimator We extract and rephrase a description of EVI in Section A.3
of the full version (Cheung et al., 2020b). EVI inputs the
Rq (s, a) 1(sq = s, aq = a)
t≠1
ÿ
r̂t (s, a) = , confidence regions Hr , Hp for the rewards and the transition
q=(· (m)≠W )‚1
Nt+ (s, a) kernels. The algorithm outputs an “optimistic MDP model”,
which consists of reward vector r̃ and transition kernel p̃
which serves to estimate the average reward under which the optimal average gain fl̃ is the largest among
all ṙ œ Hr , ṗ œ Hp :
rq (s, a)1(sq = s, aq = a)
t≠1
ÿ
r̄t (s, a) = . • Input: Confidence regions Hr for r, Hp for p, and an
Nt+ (s, a)
q=(· (m)≠W )‚1 error parameter ‘ > 0.
• Output: The returned policy fĩ and the auxiliary out-
The confidence region Hr,t = {Hr,t (s, a)}sœS,aœAs is de- put (r̃, p̃, fl̃, “˜ ). In the latter, r̃, p̃, and fl̃ are the selected
fined as “optimistic” reward vector, transition kernel, and the corre-
Hr,t (s, a) = {ṙ œ [0, 1] : |ṙ ≠ r̂t (s, a)| Æ radr,t (s, a)} , sponding long term average reward. The output “˜ œ RØ0 S
(4) is a bias vector (Jaksch et al., 2010). For each s œ S, the
with confidence radius quantity “˜ (s) is indicative of the short term reward when
the DM starts at state s and follows the optimal policy.
radr,t (s, a) = 2 2 log(SAT /”)/Nt+ (s, a). By the design of EVI, for the output “˜ , there exists s œ S
such that “˜ (s) = 0. Altogether, we express
4.3.2. C ONFIDENCE W IDENING FOR T RANSITION
K ERNELS . EVI(Hr , Hp ; ‘) æ (fĩ, r̃, p̃, fl̃, “˜ ).
For each state action pair s, a and each time step t in episode Combining the three components, a formal description of
m, consider the empirical estimator the SWUCRL2-CW algorithm is shown in Algorithm 1.
1(sq = s, aq = a, sq+1 = sÕ )
t≠1
ÿ
p̂t (sÕ |s, a) = , 4.4. Performance Analysis: The Blessing of More
q=(· (m)≠W )‚1
Nt+ (s, a) Optimism
which serves to estimate the average transition probability We now analyze the performance of the SWUCRL2-CW al-
gorithm. First, we introduce two events Er , Ep , which state
t≠1
ÿ pq (sÕ |s, a)1(sq = s, aq = a) that the estimated reward and transition kernels lie in the
p̄t (sÕ |s, a) = . respective confidence regions.
q=(· (m)≠W )‚1
Nt+ (s, a)
Er = {r̄t (s, a) œ Hr,t (s, a) ’s, a, t},
Different from the case of estimating reward, the confidence
region Hp,t (÷) = {Hp,t (s, a; ÷)}sœS,aœAs for the transi- Ep = {p̄t (·|s, a) œ Hp,t (s, a; 0) ’s, a, t}.
tion probability involves a widening parameter ÷ Ø 0:
We prove that Er , Ep hold with high probability.
Hp,t (s, a; ÷) (5) Lemma 1. We have Pr[Er ] Ø 1 ≠ ”/2, Pr[Ep ] Ø 1 ≠ ”/2.
={ṗ œ S
: Îṗ(·|s, a) ≠ p̂t (·|s, a)Î1 Æ radp,t (s, a) + ÷},
The proof is provided in Section B of the full version (Che-
with confidence radius ung et al., 2020b). In defining Ep , the widening parameterNon-Stationary Reinforcement Learning
Algorithm 1 SWUCRL2-CW algorithm Our subsequent analysis shows that ÷ can be suitably cali-
1: Input: Time horizon T , state space S, action space A, brated so that D = O(Dmax ). Next, we state our first main
window size W , widening parameter ÷. result, which provides a dynamic regret bound assuming the
2: Initialize t Ω 1, initial state s1 . knowledge of Br , Bp to set W, ÷:
3: for episode m = 1, 2, . . . do Theorem 1. Assuming S > 1, the SWUCRL2-CW algo-
4: Set · (m) Ω t, ‹m (s, a) Ω 0, and N· (m) (s, a) ac- rithm with window size W and confidence widening param-
cording to Eqn (3), for all s, a. eter ÷ > 0 satisfies the dynamic regret bound
5: Compute the confidence regions Hr,· (m) , 1 Ô Ô
Hp,· (m) (÷) according to Eqns (4, 5). Õ Bp W /÷ + Br W + SAT / W
6: Compute a 1/ · (m)-optimal optimistic policy Ë Ô Ô Ô È2
+Dmax Bp W + S AT / W + T ÷ + SAT /W + T ,
fĩm : EVI(Hr,· (m) , Hp,· (m) (÷); 1/ · (m)) æ
(fĩm , r̃m , p̃m , fl̃m , “˜m ).
with probability 1 ≠ O(”). Putting W = W ú :=
7: while t is not a multiple of W and ‹m (st , fĩm (st )) < 2 1 1 1
3S
A T /(Br + Bp + 1) and ÷ = ÷ú :=
N·+(m) (st , fĩm (st )) do
3 2 2 2
(Bp + 1)W /T , the bound specializes to
ú
8: Choose action at = fĩm (st ), observe reward
Rt (st , at ) and the next state st+1 . 1 1 2 1 3
2
Õ Dmax (Br + Bp + 1) 4 S 3 A 2 T 4 . (8)
9: Update ‹m (st , at ) Ω ‹m (st , at ) + 1, t Ω t + 1.
10: if t > T then
11: The algorithm is terminated. Proof Sketch. The complete proof is presented in Section
12: end if D of the full version (Cheung et al., 2020b). Proposition
13: end while 2 states that if the confidence region Hp,· (m) (÷) contains
14: end for a transition kernel that induces a MDP with bounded di-
ameter D, the EVI supplied with Hp,· (m) (÷) can return a
policy with controllable dynamic regret bound. However,
÷ is set to be 0, since we are only concerned with the esti- as we show in Section 6, one in general cannot expect this
mation error on p. Next, we bound the dynamic regret of to happen. Nevertheless, we bypass this with our novel
each time step, under certain assumptions on Hp,t (÷). To confidence widening technique and a budget-aware analy-
facilitate our discussion, we define the following variation sis. We consider the first time step · (m) of each episode
measure for each t in an episode m: m : if p· (m) (·|s, a) œ Hp,· (m) (s, a; ÷) for all (s, a), then
Proposition 2 can be leveraged; otherwise, the widened
t≠1
ÿ t≠1
ÿ confidence region enforces that a considerable amount of
varr,t = Br,q , varp,t = Bp,q . variation budget is consumed.
q=· (m)≠W q=· (m)≠W
Remark 2. When S = {s}, our problem becomes the
Proposition 2. Consider an episode m. Condition on non-stationary bandit problem studied by (Besbes et al.,
events Er , Ep , and suppose that there exists a transition 2014), and we have Dmax = 0 and Bp = 0. By choos-
kernel p satisfying two properties: (1) ’s œ S ’a œ As , we 2/3
ing W = W ú = A1/3 T 2/3 /Br , our algorithm has dy-
have p(·|s, a) œ Hp,· (m) (s, a; ÷), and (2) the diameter of 1/3 1/3 2/3
(S, A, p) at most D. Then, for every t œ {· (m), . . . , · (m + namic regret Õ(Br A T ), matching the minimax op-
1) ≠ 1} in episode m, we have timal dynamic regret bound by (Besbes et al., 2014) when
Br œ [A≠1 , A≠1 T ].
C D
ÿ Remark 3. Similar to (Cheung et al., 2019b), if Bp , Br
flút ≠ rt (st , at ) Æ pt (sÕ |st , at )˜
“· (m) (sÕ ) ≠ “˜· (m) (st ) are not known, wecan set W and ÷ obliviously as W =
2 1 1 2 1 1
sÕ œS
S 3 A 2 T 2 , ÷ = W/T
1 = S 3 A 2 T ≠ 2 to obtain a2dy-
(6) 2 1 3
namic regret bound Õ Dmax (Br + Bp + 1)S 3 A 2 T 4 .
1
+ + [2varr,t + 4D(varp,t + ÷)]
· (m)
# $
+ 2radr,· (m) (st , at ) + 4D · radp,· (m) (s, a) . (7)
5. Bandit-over-Reinforcement Learning:
Towards Parameter-Free
The complete proof is in Section C of the full version (Che- As said in Remark 3, in the case of unknown Br and Bp ,
ung et al., 2020b). Unlike Lemma 1, the parameter ÷ plays the dynamic regret of SWUCRL2-CW algorithm scales lin-
an important role in the Proposition. As ÷ increases, the early in Br and Bp , which leads to a (T ) dynamic regret
confidence region Hp,· (m) (s, a; ÷) becomes larger for each when Br or Bp = (T 1/4 ). In comparison, Theorem 1
s, a, and the assumed diameter D is expected to decrease. assures us that by using (W ú , ÷ ú ), we can achieve a o(T )Non-Stationary Reinforcement Learning
dynamic regret when Br , Bp = o(T ). For the bandit set- 6. The Perils of Drift in Learning Markov
ting, (Cheung et al., 2019b) proposes the bandit-over-bandit Decision Processes
framework that uses a separate copy of EXP3 algorithm
to tune the window length. Inspired by it, we develop a In stochastic online learning problems, one usually estimates
novel Bandit-over-Reinforcement Learning (BORL) algo- a latent quantity by taking the time average of observed
rithm, which is parameter free and has dynamic regret bound samples, even when the sample distribution varies across
equal to (8). Following (Cheung et al., 2019b), we view time. This has been proved to work well in stationary and
the SWUCRL2-CW algorithm as a sub-routine, and “hedge” non-stationary bandit settings (Auer et al., 2002a; Garivier
(Bubeck & Cesa-Bianchi, 2012) against the (possibly adver- & Moulines, 2011b; Cheung et al., 2019b;a). To extend to
sarial) changes of rt ’s and pt ’s to identify a reasonable fixed RL, it is natural to consider the sample average transition
window length and confidence widening parameter. As illus- distribution p̂t , which uses the data in the previous W rounds
to estimate the time average transition distribution p̄t to
within an additive error Õ(1/ Nt+ (s, a)) (see Lemma 1).
In the case of stationary MDPs, where ’ t œ [T ] pt = p,
one has p̄t = p. Thus, the un-widened confidence region
Hp,t (0) contains p with high probability (see Lemma 1).
Consequently, the UCRL2 algorithm by (Jaksch et al., 2010),
which optimistic explores Hp,t (0), has a regret that scales
linearly with the diameter of p.
The approach of optimistic exploring Hp,t (0) is further ex-
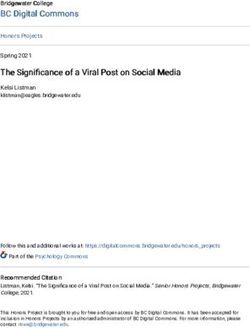
Figure 1. Structure of the BORL algorithm tended to RL in piecewise-stationary MDPs by (Jaksch
et al., 2010; Gajane et al., 2018). The latter establishes a
2/3
O(¸1/3 Dmax S 2/3 A1/3 T 2/3 ) dynamic regret bounds, when
trated in Fig. 1, the BORL algorithm divides the whole time there are at most ¸ changes. Their analyses involve partition-
horizon into ÁT /HË blocks of equal length H rounds (the ing the T -round horizon into C · T 1/3 equal-length intervals,
length of the last block can Æ H), and specifies a set J from where C is a constant dependent on Dmax , S, A, ¸. At least
which each pair of (window length, confidence widening pa- CT 1/3 ≠¸ intervals enjoy stationary environments, and opti-
rameter) are drawn from. For each block i œ [ÁT /HË], the mistic exploring Hp,t (0) in these intervals yields a dynamic
BORL algorithm first calls some master algorithm to select regret bound that scales linearly with Dmax . Bounding the
a pair of (window length, confidence widening parameter) dynamic regret of the remaining intervals by their lengths
(Wi , ÷i ) œ J, and restarts the SWUCRL2-CW algorithm with and tuning C yield the desired bound.
the selected parameters as a sub-routine to choose actions
for this block. Afterwards, the total reward of block i is fed In contrast to the stationary and piecewise-stationary set-
back to the master, and the “posterior” of these parameters tings, optimistic exploration on Hp,t (0) might lead to unfa-
are updated accordingly. vorable dynamic regret bounds in non-stationary MDPs. In
the non-stationary environment where pt≠W , . . . , pt≠1 are
One immediate challenge not presented in the bandit setting generally distinct, we show that it is impossible to bound the
(Cheung et al., 2019b) is that the starting state of each block diameter of p̄t in terms of the maximum of the diameters of
is determined by previous moves of the DM. Hence, the pt≠W , . . . , pt≠1 . More generally, we demonstrate the pre-
master algorithm is not facing a simple oblivious environ- vious claim not only for p̄t , but also for every p̃ œ Hp,t (0)
ment as the case in (Cheung et al., 2019b), and we cannot in the following Proposition. The Proposition showcases
use the EXP3 (Auer et al., 2002b) algorithm as the master. the unique challenge in exploring non-stationary MDPs that
Nevertheless, the state is observed before the starting of a is absent in the piecewise-stationary MDPs, and motivates
block. Thus, we use the EXP3.P algorithm for multi-armed our notion of confidence widening with ÷ > 0. To ease the
bandit against an adaptive adversary (Auer et al., 2002b) as notation, we put t = W + 1 without loss of generality.
the master algorithm. Owing to its similarity to the BOB
algorithm (Cheung et al., 2019b), we defer the design de- Proposition 3. There exists a sequence of non-stationary
tails and the proof of dynamic regret bound for the BORL MDP transition distributions p1 , . . . , pW such that 1) The
algorithm to Sections E and F of the full version (Cheung diameter of (S, A, pn ) is 1 for each n œ [W ]. 2) The total
et al., 2020b), respectively. variations in state transition distributions is O(1). Never-
theless, under some deterministic policy,
Theorem 2. Assume S > 1, with probability 1 ≠ O(”), • The empirical MDP (S, A, p̂W +1 ) has diameter (W )
the dynamic regret bound of the BORL algorithm is
1 2 1 3 p̃ œ Hp,W +1 (0), the MDP (S, A, p̃)
• Further, for every
Õ(Dmax (Br + Bp + 1) 4 S 3 A 2 T 4 ). has diameter ( W/ log W )Non-Stationary Reinforcement Learning
Proof. The sequence p1 , . . . , pW alternates between the fol-
lowing 2 instances p1 , p2 . Now, define the common state
space S = {1, 2} and action collection A = {A1 , A2 },
where A1 = {a1 , a2 }, {A2 } = {b1 , b2 }. We assume all
the state transitions are deterministic, and a graphical illus-
tration is presented in Fig. 2. Clearly, we see that both
instances have diameter 1.
Figure 3. (From top to bottom) Underlying policies, transition ker-
nels, time steps, and state visits.
Finally, for the confidence region Hp,W +1 (0) =
{Hp,W +1 (s, a; 0)}s,a constructed without confidence
widening, for any p̃ œ Hp,W +1 (0) we have p̃(2|1, a1 ) =
1Ò 2
log W
p̃(1|2, b1 ) = O · +1 and p̃(2|1, a2 ) = p̃(1|2, b2 ) =
1Ò 2
Figure 2. Example MDPs (with deterministic transitions). log W
O · ≠1 respectively, since the stochastic confidence
1Ò 2 1Ò 2
Now, consider the following two deterministic and station- log W log W
radii and dominate the sample
ary policies fi 1 and fi 2 : fi 1 (1) = a1 , fi 1 (2) = b2 , fi 2 (1) = · +1 · ≠1
1
a2 , fi 2 (2) = b1 . Since the MDP is deterministic, we have mean · +1 and 0. Therefore, for any p̃ œ Hp,W +1 (0), the
p̂W +1 = p̄W +1 . diameter
1Ò of 2the MDP constructed by (S, A, p̃) is at least
W
log W .
In the following, we construct a trajectory where the DM
alternates between policies fi 1 , fi 2 during time {1, . . . , W } Remark 4. Inspecting the prevalent OFU guided approach
while the underlying transition kernel alternates between for stochastic MAB and RL in MDPs settings (Auer et al.,
p1 , p2 . In the construction, the DM is almost always at the 2002a; Abbasi-Yadkori et al., 2011; Jaksch et al., 2010;
self-loop at state 1 (or 2) throughout the horizon, no matter Bubeck & Cesa-Bianchi, 2012; Lattimore & Szepesvári,
what action a1 , a2 (or b1 , b2 ) she takes. Consequently, it 2018), one usually concludes that a tighter design of confi-
will trick the DM into thinking that p̂W +1 (1|1, ai ) ¥ 1 for dence region can result in a lower (dynamic) regret bound.
each i œ {1, 2}, and likewise p̂W +1 (2|2, bi ) ¥ 1 for each In (Abernethy et al., 2016), this insights has been formal-
i œ {1, 2}. Altogether, this will lead the DM to conclude ized in stochastic K-armed bandit settings via a potential
that (S, A, p̂W +1 ) constitute a high diameter MDP, since function type argument. Nevertheless, Proposition 3 (to-
the probability of transiting from state 1 to 2 (and 2 to 1) gether with Theorem 1) demonstrates that using the tightest
are close to 0. confidence region in learning algorithm design may not
The construction is detailed as follows. Let W = 4· . In be enough to ensure low dynamic regret bound for RL in
addition, let the state transition kernels be p1 from time 1 non-stationary MDPs.
to · and from time step 2· + 1 to 3· and be p2 for the
remaining time steps. The DM starts at state 1. She follows 7. Conclusion
policy fi 1 from time 1 to time 2· , and policy fi 2 from 2· + 1
to 4· . Under the specified instance and policies, it can be In this paper, we studied the problem of non-stationary re-
readily verified that the DM takes inforcement learning where the unknown reward and state
transition distributions can be different from time to time
• action a1 from time 1 to · + 1, as long as the total changes are bounded by some variation
• action b2 from time · + 2 to 2· , budgets, respectively. We first incorporated the sliding win-
• action b1 from time 2· + 1 to 3· + 1, dow estimator and the novel confidence widening technique
• action a2 from time 3· + 2 to 4· . into the UCRL2 algorithm to propose the SWUCRL2-CW
As a result, the DM is at state 1 from time 1 to · + 1, and algorithm with low dynamic regret when the variation bud-
time 3· + 2 to 4· ; while she is at state 2 from time · + 2 to gets are known. We then designed the parameter-free BORL
3· + 1, as depicted in Fig. 3. We have: algorithm that allows us to enjoy this dynamic regret bound
· 1 without knowing the variation budgets. The main ingredient
p̂W +1 (1|1, a1 ) = , p̂W +1 (2|1, a1 ) = of the proposed algorithms is the novel confidence widening
· +1 · +1
technique, which injects extra optimism into the design of
p̂W +1 (1|1, a2 ) = 1, p̂W +1 (2|1, a2 ) = 0 learning algorithms. This is in contrast to the widely held
· 1 believe that optimistic exploration algorithms for (station-
p̂W +1 (2|2, b1 ) = , p̂W +1 (1|2, b1 ) =
· +1 · +1 ary and non-stationary) stochastic online learning settings
p̂W +1 (2|2, b2 ) = 1, p̂W +1 (1|2, b2 ) = 0. should employ the lowest possible level of optimism.Non-Stationary Reinforcement Learning
Acknowledgements Cai, H., Ren, K., Zhang, W., Malialis, K., Wang, J., Yu, Y.,
and Guo, D. Real-time bidding by reinforcement learn-
The authors would like to express sincere gratitude to Dy- ing in display advertising. In Proceedings of the ACM
lan Foster, Negin Golrezaei, and Mengdi Wang, as well International Conference on Web Search and Data Mining
as various seminar attendees for helpful discussions and (WSDM), 2017.
comments. Cardoso, A. R., Wang, H., and Xu, H. Large scale markov decision
processes with changing rewards. In Advances in Neural
Information Processing Systems 32 (NeurIPS), 2019.
References Chen, W., Shi, C., and Duenyas, I. Optimal learning algorithms
Abbasi-Yadkori, Y., Pál, D., and Szepesvári, C. Improved algo- for stochastic inventory systems with random capacities. In
rithms for linear stochastic bandits. In Advances Neural SSRN Preprint 3287560, 2019a.
Information Processing Systems 25 (NIPS), 2011. Chen, Y., Lee, C.-W., Luo, H., and Wei, C.-Y. A new algorithm for
Abbasi-Yadkori, Y., Bartlett, P. L., Kanade, V., Seldin, Y., and non-stationary contextual bandits: Efficient, optimal, and
Szepesvári, C. Online learning in markov decision processes parameter-free. In Proceedings of Conference on Learning
with adversarially chosen transition probability distributions. Theory (COLT), 2019b.
In Advances in Neural Information Processing Systems 26 Cheung, W. C., Simchi-Levi, D., and Zhu, R. Learning to optimize
(NIPS), 2013. under non-stationarity. In Proceedings of International Con-
Abernethy, J., Amin, K., and Zhu, R. Threshold bandits, with ference on Artificial Intelligence and Statistics (AISTATS),
and without censored feedback. In Advances in Neural 2019a.
Information Processing Systems 29 (NIPS), 2016. Cheung, W. C., Simchi-Levi, D., and Zhu, R. Hedging the
Agrawal, S. and Jia, R. Optimistic posterior sampling for rein- drift: Learning to optimize under non-stationarity. In
forcement learning: worst-case regret bounds. In Advances arXiv:1903.01461, 2019b. URL https://arxiv.org/
in Neural Information Processing Systems 30 (NIPS), pp. abs/1903.01461.
1184–1194. Curran Associates, Inc., 2017. Cheung, W. C., Simchi-Levi, D., and Zhu, R. Non-stationary
Agrawal, S. and Jia, R. Learning in structured mdps with con- reinforcement learning: The blessing of (more) optimism.
vex cost functions: Improved regret bounds for inventory In arXiv:1906.02922v4 [cs.LG], 2020a. URL https://
management. In Proceedings of the ACM Conference on arxiv.org/abs/1906.02922.
Economics and Computation (EC), 2019. Cheung, W. C., Simchi-Levi, D., and Zhu, R. Reinforcement
Arora, R., Dekel, O., and Tewari, A. Deterministic mdps with learning for non-stationary markov decision processes: The
adversarial rewards and bandit feedback. In Proceedings of blessing of (more) optimism. In arXiv:2006.14389, 2020b.
the Twenty-Eighth Conference on Uncertainty in Artificial URL https://arxiv.org/abs/2006.14389.
Intelligence, pp. 93–101, 2012. Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. Intro-
Auer, P., Cesa-Bianchi, N., and Fischer, P. Finite-time analysis of duction to algorithms. In MIT Press, 2009.
the multiarmed bandit problem. In Machine learning, 47, Dick, T., György, A., and Szepesvári, C. Online learning in markov
235–256, 2002a. decision processes with changing cost sequences. In Pro-
Auer, P., Cesa-Bianchi, N., Freund, Y., and Schapire, R. The ceedings of the International Conference on Machine Learn-
nonstochastic multiarmed bandit problem. In SIAM Journal ing (ICML), 2014.
on Computing, 2002, Vol. 32, No. 1 : pp. 48–77, 2002b. Even-Dar, E., Kakade, S. M., , and Mansour, Y. Experts in a
Balseiro, S. and Gur, Y. Learning in repeated auctions with bud- markov decision process. In Advances in Neural Informa-
gets: Regret minimization and equilibrium. In Management tion Processing Systems 18 (NIPS), 2005.
Science, 2019. Flajolet, A. and Jaillet, P. Real-time bidding with side information.
Bartlett, P. L. and Tewari, A. REGAL: A regularization based algo- In Advances in Neural Information Processing Systems 30
rithm for reinforcement learning in weakly communicating (NeurIPS), 2017.
mdps. In UAI 2009, Proceedings of the Twenty-Fifth Con- Fruit, R., Pirotta, M., and Lazaric, A. Near optimal exploration-
ference on Uncertainty in Artificial Intelligence, Montreal, exploitation in non-communicating markov decision pro-
QC, Canada, June 18-21, 2009, pp. 35–42, 2009. cesses. In Advances in Neural Information Processing Sys-
Bertsekas, D. Dynamic Programming and Optimal Control. tems 31, pp. 2998–3008. Curran Associates, Inc., 2018a.
Athena Scientific, 2017. Fruit, R., Pirotta, M., Lazaric, A., and Ortner, R. Efficient bias-
Besbes, O., Gur, Y., and Zeevi, A. Stochastic multi-armed ban- span-constrained exploration-exploitation in reinforcement
dit with non-stationary rewards. In Advances in Neural learning. In Proceedings of the 35th International Confer-
Information Processing Systems 27 (NIPS), 2014. ence on Machine Learning, volume 80 of Proceedings of
Bimpikis, K., Candogan, O., and Saban, D. Spatial pricing in Machine Learning Research, pp. 1578–1586. PMLR, 10–15
ride-sharing networks. In Operations Research, 2019. Jul 2018b.
Bubeck, S. and Cesa-Bianchi, N. Regret Analysis of Stochastic and Fruit, R., Pirotta, M., and Lazaric, A. Improved analysis of ucrl2b.
Nonstochastic Multi-armed Bandit Problems. Foundations In https://rlgammazero.github.io/, 2019.
and Trends in Machine Learning, 2012, Vol. 5, No. 1: pp. Gajane, P., Ortner, R., and Auer, P. A sliding-window algorithm
1–122, 2012. for markov decision processes with arbitrarily changing
Burnetas, A. N. and Katehakis, M. N. Optimal adaptive policies for rewards and transitions. 2018.
markov decision processes. In Mathematics of Operations Garivier, A. and Moulines, E. On upper-confidence bound policies
Research, volume 22, pp. 222–255, 1997. for switching bandit problems. In Proceedings of Interna-Non-Stationary Reinforcement Learning
tional Conferenc on Algorithmic Learning Theory (ALT), Neu, G., Gyorgy, A., and Szepesvari, C. The adversarial stochastic
2011a. shortest path problem with unknown transition probabilities.
Garivier, A. and Moulines, E. On upper-confidence bound policies In Proceedings of the Fifteenth International Conference
for switching bandit problems. In Algorithmic Learning on Artificial Intelligence and Statistics, volume 22, pp. 805–
Theory, pp. 174–188. Springer Berlin Heidelberg, 2011b. 813. PMLR, 21–23 Apr 2012.
Guo, X., Hu, A., Xu, R., and Zhang, J. Learning mean-field games. Nowzari, C., Preciado, V. M., and Pappas, G. J. Analysis and
In Advances in Neural Information Processing Systems 32 control of epidemics: A survey of spreading processes on
(NeurIPS), 2019. complex networks. In IEEE Control Systems Magazine,
2016.
Gurvich, I., Lariviere, M., and Moreno, A. Operations in the on-
demand economy: Staffing services with self-scheduling Ortner, R., Gajane, P., and Auer, P. Variational regret bounds for
capacity. In Sharing Economy: Making Supply Meet De- reinforcement learning. In Proceedings of Conference on
mand, 2018. Uncertainty in Artificial Intelligence (UAI), 2019.
Han, Y., Zhou, Z., and Weissman, T. Optimal no-regret learning in Puterman, M. L. Markov Decision Processes: Discrete Stochastic
repeated first-price auctions. In arXiv:2003.09795, 2020. Dynamic Programming. John Wiley & Sons, Inc., New
York, NY, USA, 1st edition, 1994.
Hoeffding, W. Probability inequalities for sums of bounded ran-
dom variables. In Journal of the American statistical as- Qin, Z. T., Tang, J., and Ye, J. Deep reinforcement learning with
sociation, volume 58, pp. 13–30. Taylor & Francis Group, applications in transportation. In Tutorial of the 33rd AAAI
1963. Conference on Artificial Intelligence (AAAI-19), 2019.
Huh, W. T. and Rusmevichientong, P. A nonparametric asymptotic Rosenberg, A. and Mansour, Y. Online convex optimization in
analysis of inventory planning with censored demand. In adversarial Markov decision processes. In Proceedings of
Mathematics of Operations Research, 2009. the 36th International Conference on Machine Learning,
volume 97, pp. 5478–5486. PMLR, 2019.
Jaksch, T., Ortner, R., and Auer, P. Near-optimal regret bounds for
reinforcement learning. In J. Mach. Learn. Res., volume 11, Shortreed, S., Laber, E., Lizotte, D., Stroup, S., and Murphy, J.
pp. 1563–1600. JMLR.org, August 2010. P. S. Informing sequential clinical decision-making through
reinforcement learning: an empirical study. In Machine
Jin, C., Jin, T., Luo, H., Sra, S., and Yu, T. Learning adversar- Learning, 2010.
ial markov decision processes with bandit feedback and
unknown transition. 2019. Sidford, A., Wang, M., Wu, X., Yang, L. F., and Ye, Y. Near-
optimal time and sample complexities for solving dis-
Kanoria, Y. and Qian, P. Blind dynamic resource alloca- counted markov decision process with a generative model.
tion in closed networks via mirror backpressure. In In Advances in Neural Information Processing Systems 31
arXiv:1903.02764, 2019. (NeurIPS), 2018a.
Karnin, Z. and Anava, O. Multi-armed bandits: Competing with Sidford, A., Wang, M., Wu, X., and Ye, Y. Variance reduced
optimal sequences. In Advances in Neural Information value iteration and faster algorithms for solving markov
Processing Systems 29 (NIPS), 2016. decision processes. In Proceedings of the Annual ACM-
Keskin, N. and Zeevi, A. Chasing demand: Learning and earning SIAM Symposium on Discrete Algorithms (SODA), 2018b.
in a changing environments. In Mathematics of Operations Sutton, R. S. and Barto, A. G. Reinforcement Learning: An
Research, 2016, 42(2), 277–307, 2016. Introduction. A Bradford Book, 2018.
Kim, M. J. and Lim, A. E. Robust multiarmed bandit problems. In Taylor, T. On-demand service platforms. In Manufacturing &
Management Science, 2016. Service Operations Management, 2018.
Kiss, I. Z., Miller, J. C., and Simon, P. L. Mathematics of epidemics Tewari, A. and Bartlett, P. L. Optimistic linear programming
on networks. In Springer, 2017. gives logarithmic regret for irreducible mdps. In Advances
Kveton, B., Wen, Z., Ashkan, A., and Szepesvári, C. Tight re- in Neural Information Processing Systems 20 (NIPS), pp.
gret bounds for stochastic combinatorial semi-bandits. In 1505–1512. 2008.
AISTATS, 2015. Wang, M. Randomized linear programming solves the markov
Lattimore, T. and Szepesvári, C. Bandit Algorithms. Cambridge decision problem in nearly-linear (sometimes sublinear)
University Press, 2018. running time. In Mathematics of Operations Research,
Li, Y., Zhong, A., Qu, G., and Li, N. Online markov decision 2019.
processes with time-varying transition probabilities and re- Wei, C.-Y., Jafarnia-Jahromi, M., Luo, H., Sharma, H., and
wards. In ICML workshop on Real-world Sequential Deci- Jain, R. Model-free reinforcement learning in infinite-
sion Making, 2019. horizon average-reward markov decision processes. In
Luo, H., Wei, C., Agarwal, A., and Langford, J. Efficient con- arXiv:1910.07072, 2019.
textual bandits in non-stationary worlds. In Proceedings of Xu, K. and Yun, S.-Y. Reinforcement with fading memories. In
Conference on Learning Theory (COLT), 2018. Mathematics of Operations Research, 2020.
Ma, W. Improvements and generalizations of stochastic knap- Yu, J. Y. and Mannor, S. Online learning in markov decision
sack and markovian bandits approximation algorithms. In processes with arbitrarily changing rewards and transitions.
Mathematics of Operations Research, 2018. In Proceedings of the International Conference on Game
Neu, G., Antos, A., György, A., and Szepesvári, C. Online markov Theory for Networks, 2009.
decision processes under bandit feedback. In Advances Yu, J. Y., Mannor, S., and Shimkin, N. Markov decision pro-
in Neural Information Processing Systems 23 (NIPS), pp. cesses with arbitrary reward processes. In Mathematics of
1804–1812. 2010. Operations Research, volume 34, pp. 737–757, 2009.Non-Stationary Reinforcement Learning
Zhang, A. and Wang, M. Spectral state compression of markov
processes. In arXiv:1802.02920, 2018.
Zhang, H., Chao, X., and Shi, C. Closing the gap: A learning
algorithm for the lost-sales inventory system with lead times.
In Management Science, 2018.
Zhang, Z. and Ji, X. Regret minimization for reinforcement learn-
ing by evaluating the optimal bias function. In Advances
in Neural Information Processing Systems 32 (NeurIPS),
2019.
Zhou, X., Chen, N., Gao, X., and Xiong, Y. Regime switching
bandits. In arXiv:2001.09390, 2020.
Zhou, Z. and Bambos, N. Wireless communications games in
fixed and random environments. In IEEE Conference on
Decision and Control (CDC), 2015.
Zhou, Z., Glynn, P., and Bambos, N. Repeated games for power
control in wireless communications: Equilibrium and regret.
In IEEE Conference on Decision and Control (CDC), 2016.You can also read